Handicap Toilet Stalls

collage of items

Diz

By David Abraham Rodriguez Rivera and Gerardo Perez Yazbeth

Meatl Core Scooter Wheels

Bodies

A prism in geometry, a polyhedron composed of two equal and parallel faces called bases, and lateral faces are parallelograms.
In the case where the sides are rectangular prism is called rectogularino. The rectangular prism or cuboid, and the octagonal prism are among the types of prism with a rectangular base and octagon, respectively.

irregular prisms
their bases are irregular polygons. Roof prism

The sides of a prism are rectangles or squares .

The height of a prism coincides with its lateral edge.

An oblique prism oblique prism is a prism whose lateral edges are angled cross or the horizontal desviadode
bases
Parallelepiped
is a polyhedron with six faces (thus, a hexahedron), in which all faces are parallelograms, and parallel and equal in pairs.
A parallelepiped has 12 edges, which are equal and parallel in groups of four, and 8 vertices.

M Jak Milosc Nowe Odcinki

round prisms and pyramids

revolution Solid

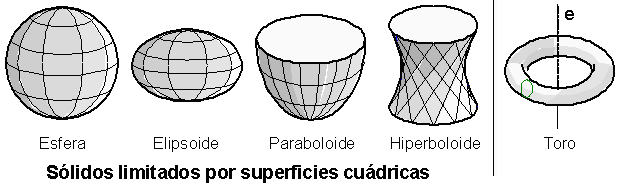
Round body limited by a generator (g) curve, which rotates around an axis (e). These may include:

• solid surfaces limitdos by quadrics :
  • area: the generating station is a circle,
  • ellipsoid: the generating station is an ellipse,
  • paraboloid: the generating station is a parable,
  • hyperboloid: the generating station is a hyperbola,
• torus (ring) . Its surface is generated by a circle or an ellipse, which revolves around an axis (e), coplanar with it, and outside it.

Cylinder

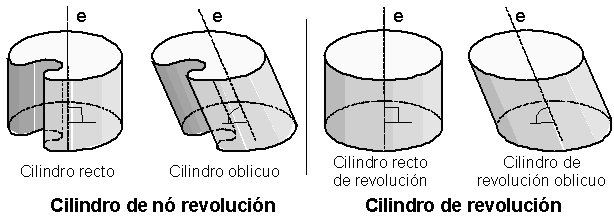
Round body limited by a cylindrical surface and two parallel flat bases. The line through the geometric centers of the bases is called the cylinder axis (e), and is parallel to the generatrix (g) of the cylindrical surface. Cylinders can be:

• right cylinder: if the axis (e) is perpendicular to the bases,
• Cilinder oblique ro: if the axis (e) is not perpendicular to the bases,
• c ilindro revolution: If you are limited by a cylindrical surface of revolution. Can in turn be:
  
  
  • straight cylinder revolution: if the axis (e) is perpendicular to the bases,
  • oblique cylinder revolution : if the axis (e) is not perpendicular to the bases.
• 
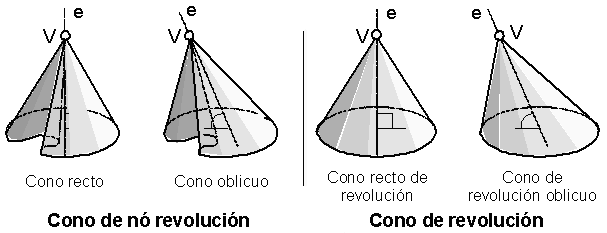
  Cone Round body limited by a conical surface and a flat base. The line through the vertex (V) of the conical surface and the geometric center of the base is called the cone axis (e). The cones can be:
• right cone: if the axis (e) is perpendicular to the base,
• oblique cone: if the axis (e) is not perpendicular to the base,
• cone of revolution : If you are limited by a conical surface of revolution. Can in turn be:
  • right cone of revolution : if the axis (e) is perpendicular to the base,
  • oblique cone of revolution : if the axis (e ) is not perpendicular to the base.

Average Food And Drink Prices In Krakow 2010

revolution

A pyramid is a polyhedron bounded by a base, which is a polygon any, and faces that are triangles coincident at a point called the apex.
The apex or top is also called the vertex of the pyramid, while a pyramid has more vertices, as many as the number of polygons that limit. Types

pyramids

straight A pyramid is a type of pyramid whose lateral faces are isosceles triangles. In this type of pyramid perpendicular to the base line passing through the apex to the base cut its circumcenter. Oblique
-A pyramid is one in which not all sides are isosceles triangles.
-A regular pyramid is a pyramid straight whose base is a regular polygon.

-A pyramid is based on a convex polygon convex and concave pyramid's base is a concave polygon.
There are three types of pyramids whose faces are equilateral triangles, with bases of 3, 4 and 5 sides respectively. A tetrahedron is a pyramid whose sides (base and sides) are equilateral triangles.

How To Get Rid Of A Bad Chest Infection

The Platonic solids are the tetrahedron, the cube (or hexahedron regular), the octahedron, the dodecahedron and the icosahedron. Also known as Platonic bodies, bodies cosmic Pythagorean solids, solid perfect, Plato's polyhedra or, more accurately, convex regular polyhedra. Are characterized by convex polyhedra whose faces are equal regular polygons and whose vertices are attached to the same number of faces. Given these names after the Greek philosopher Plato (ca . AdC/428 427 BC - 347 BC), who is credited if any studied in the first instance. Properties

Regularity

As has been stated for define these polyhedra:

• All faces of a Platonic solid are equal regular polygons.
• In all the vertices of a Platonic solid attend the same number of faces and edges.
• All edges of a Platonic solid are the same length.
• All dihedral angles formed by the faces of a Platonic solid with each other are equal.
• All its vertices are convex to the icosahedron.

Symmetry

The Platonic solids are highly symmetrical:

• All of them are central symmetry about a point space (center of symmetry) which is equidistant from their faces, vertices and edges.
• They also have axial symmetry on a number of axes of symmetry passing through the center of symmetry above.
• They also have mirror symmetry about a series of planes of symmetry (or principal planes), which divided into two equal parts.

geometric Following the above, can be traced all Platonic solid three particular areas, all focused in the center of symmetry of the polyhedron:

• A sphere inscribed tangent to all sides in the middle.
• A second sphere tangent to all edges in the center.
• A circumscribed sphere, passing through all vertices of the polyhedron.

projecting the centers of the edges of a Platonic polyhedron circumscribed about the sphere from the center of symmetry of the polyhedron is obtained a regular spherical network, composed of equal-circle arcs, which are regular spherical polygons.

polyhedra whose faces are equal regular polygons are called regular polyhedra . There are five regular polyhedrons:

hexahedron (6 square):

A cube or regular hexahedron is a polyhedron with six congruent square faces, one of the so-called Platonic solids.
A cube, and is a hexahedron, may also be classified as a parallelepiped rectangle straight, because all sides are parallel sides and four pairs, and even as a prism with square base and height equal to the side of the base.

tetrahedron (4 triangles equilateral) :

A tetrahedron is a polyhedron with four faces. With this number of heads is bound to be a convex polyhedron, and triangular faces, meeting three in each corner. If the four faces of the tetrahedron are equilateral triangles, necessarily equal to each other, the tetrahedron is called regular. The tetrahedron is the three-dimensional simplex.

Dodecahedron (12 regular pentagons)

A dodecahedron is a twelve-sided polyhedron, convex or concave. Their faces are to be polygon of eleven sides or less. If the twelve faces of the dodecahedron are regular pentagons necessarily equal to each other, the dodecahedron is convex and is called regular, then being a so-called Platonic solids.

Icosahedron (20 equilateral triangles)

An icosahedron is a twenty-sided polyhedron, convex or concave. Their faces are to be nineteen-sided polygons or less. If the twenty faces of the icosahedron are equilateral triangles, necessarily equal to each other, the icosahedron is convex and is called regular , being then a so-called Platonic solids. The conjugate polyhedron of the icosahedron is the dodecahedron.

Octahedron (8 triangles equilateral)

An octahedron is a polyhedron with eight faces. With this number of faces can be a convex polyhedron or a concave polyhedron. Their faces are to be seven-sided polygons or less. If the eight faces of the octahedron are equilateral triangles, necessarily equal to each other, the octahedron is convex and is called regular , being then a so-called Platonic solids.

Zatrzymać Meczety